Machine learning for PinT methods
Machine learning based approaches have proven very successful within certain problem settings, in particular in imaging. Lately also more and more successes for solving partial differential equations have been reported, e.g., by using pyhsics-informed neural networks, or to improve coarse-grid simulations by learned corrections. In this project we will investigate approaches to facilitate such techniques to improve performance of parallel-in-time methods.
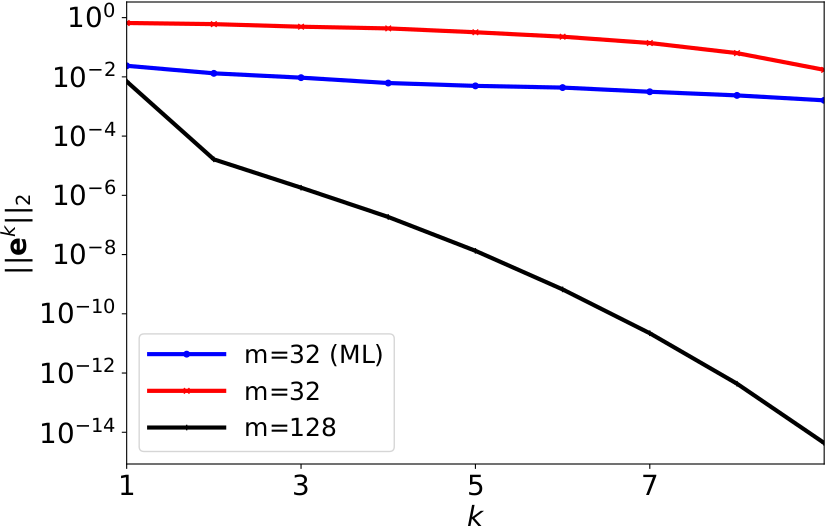
Coarsening in space is known to reduce Parareals convergence speed for hyperbolic PDEs. Initial attempts to counteract this effect using machine learning show an reduced error with a learned coarse propagator, and potential speedup, but no improved convergence speed. Similar results are achieved for a trained correction/interpolation from coarse to fine grid. Using more information about the PDE to be solved, e.g., using PINNs (physics-informed neural networks) might further reduce the error.
